變壓器鐵芯磁致伸縮計(jì)算分析
作者:威博特鐵芯 發(fā)布時(shí)間:2019-03-30 15:05:47 瀏覽次數(shù): 電磁噪聲是變壓器特別是干式變壓器噪聲的主要組成部分, 而硅鋼片磁致伸縮效應(yīng)是引起電磁噪聲的主要原因。 所以對(duì)鐵芯硅鋼片磁致伸縮特性進(jìn)行數(shù)值計(jì)算分析, 從振源方面對(duì)變壓器進(jìn)一步降噪具有重要意義。
所謂磁致伸縮是指鐵磁物質(zhì)(磁性材料)由于磁化狀態(tài)的改變,其尺寸在各個(gè)方向發(fā)生變化。組成變壓器鐵芯的硅鋼片,被磁化時(shí)發(fā)生磁致伸縮現(xiàn)象,屬于磁致伸縮材料。 在理想實(shí)驗(yàn)條件下硅鋼片的磁致伸縮量很小, 但由于磁致伸縮諧波頻率與鐵芯固有頻率發(fā)生共振等原因, 它在鐵芯中引起的振動(dòng)被放大, 由此產(chǎn)生的噪聲也是變壓器本體噪聲的主要來(lái)源。
本文中基于不同應(yīng)力作用下鐵芯的磁化曲線, 依據(jù)考慮鐵芯磁致伸縮特性的電磁—機(jī)械振動(dòng)耦合數(shù)值模型, 計(jì)算實(shí)現(xiàn)了每個(gè)單元的磁致伸縮應(yīng)力、應(yīng)變數(shù)值分布,并進(jìn)一步計(jì)算了局部磁致伸縮力和電磁力的大小, 通過(guò)相關(guān)對(duì)比驗(yàn)證了結(jié)果的正確性。 文中的分析計(jì)算方法具有普遍應(yīng)用性。
1、硅鋼片磁致伸縮特性
鐵芯磁化發(fā)生磁致伸縮現(xiàn)象, 硅鋼片的磁致伸縮對(duì)所受機(jī)械應(yīng)力很敏感。 但不同方向的應(yīng)力影響不同,沿軋制方向磁化的取向硅鋼片,拉應(yīng)力對(duì)其的磁致伸縮影響甚小,而壓應(yīng)力影響很大,如圖1 中任意曲線所示。
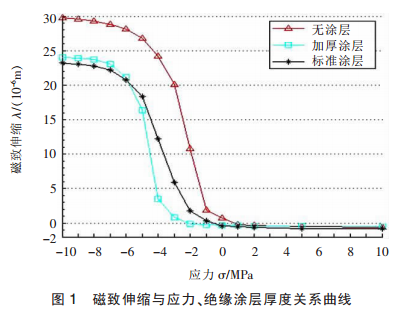
另外, 近期研究發(fā)現(xiàn)硅鋼片的磁致伸縮也會(huì)隨硅鋼片厚度的增加而增大[11]。 不同廠商、不同型號(hào)的硅鋼片具有不同的磁致伸縮變化,到現(xiàn)在為止,仍沒(méi)有準(zhǔn)確描述商業(yè)硅鋼片磁致伸縮與應(yīng)力對(duì)應(yīng)關(guān)系,所以對(duì)硅鋼片磁致伸縮效應(yīng)的數(shù)值計(jì)算需測(cè)量磁致伸縮特性在不同應(yīng)力作用下的數(shù)據(jù)。
2、鐵芯電磁—機(jī)械振動(dòng)耦合數(shù)值模型
磁致伸縮材料的本構(gòu)關(guān)系方程可明確表示磁場(chǎng)與機(jī)械場(chǎng)相互耦合的關(guān)系:

σ——應(yīng)力
Eσ——楊氏模量
Bσ——σ 作用的磁感應(yīng)強(qiáng)度
μσ——在應(yīng)力作用下的磁導(dǎo)率
d——磁致伸縮系數(shù)
由于鐵芯硅鋼片磁致伸縮的峰值也只有幾微米大小,可知它的磁致伸縮系數(shù)甚小。而鐵芯硅鋼片在應(yīng)力作用下導(dǎo)磁曲線將發(fā)生變化,鐵芯被磁化時(shí)自然發(fā)生磁致伸縮,因此,采用在應(yīng)力作用下測(cè)量的硅鋼片 B-H 曲線可同時(shí)考慮應(yīng)力、 磁致伸縮的影響,式(1)和式(2)可表示為:

由此可知,考慮硅鋼片磁致伸縮應(yīng)力影響,求解變壓器鐵芯區(qū)域磁場(chǎng)的麥克斯韋方程為式(4):

J——z 方向激磁電流密度
本文中采用松耦合數(shù)值模型計(jì)算電磁場(chǎng)和機(jī)械場(chǎng),變壓器鐵芯的電磁場(chǎng)和機(jī)械場(chǎng)分別由式(5)、式(6)來(lái)表示:

K——機(jī)械剛度矩陣
A、U——要求解的磁場(chǎng)矢量和振動(dòng)位移矩陣
兩式通過(guò)磁致伸縮效應(yīng)引起鐵芯硅鋼片磁導(dǎo)率的變化,以及磁場(chǎng)作用引起磁致伸縮,從而對(duì)機(jī)械變形產(chǎn)生影響來(lái)實(shí)現(xiàn)磁性和彈性領(lǐng)域的耦合。
采用有限元進(jìn)行計(jì)算時(shí),分別利用電磁場(chǎng)、機(jī)械場(chǎng)的能量泛函來(lái)離散求解電磁和機(jī)械的剛度矩陣,單元泛函表達(dá)式如下:


采用有限元進(jìn)行單元分析時(shí), 每個(gè)單元內(nèi)的磁通密度恒定。硅鋼片被磁化時(shí),發(fā)生磁致伸縮引起內(nèi)應(yīng)力發(fā)生變化,磁導(dǎo)率隨之變化,進(jìn)而影響磁能的大小。根據(jù)虛功原理,硅鋼片的磁致伸縮力等于因磁致伸縮效應(yīng)引起的磁能變化與振動(dòng)位移的相對(duì)變化,單元磁致伸縮力求解表達(dá)式如式(10)所示:


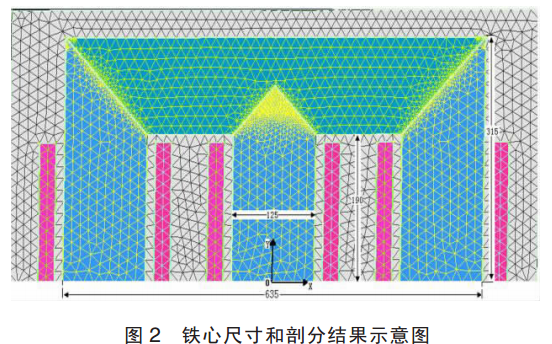
本文中筆者選用三相三柱電力變壓器作為分析對(duì)象,變壓器工作在空載狀態(tài),依據(jù)磁路方法采用等效拼接間隙 δ 計(jì)及搭迭效應(yīng)。 采用 Femap 前處理軟件對(duì)變壓器 2D 對(duì)稱(chēng)模型進(jìn)行剖分, 其鐵芯尺寸和剖分結(jié)果如圖 2 所示,共含有 6 233 個(gè)單元,1 195個(gè)節(jié)點(diǎn)。
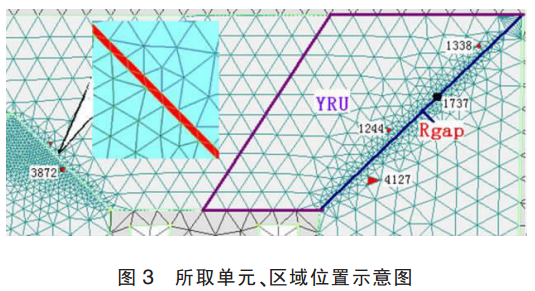
由圖 4 可知, 應(yīng)力、 應(yīng)變周期為磁場(chǎng)周期的一半;硅鋼片沿軋制方向的應(yīng)力、應(yīng)變遠(yuǎn)大于沿垂直軋制方向的應(yīng)力、應(yīng)變,符合硅鋼片磁致伸縮的特性,量級(jí)也與測(cè)量值相符。 電磁應(yīng)力 X 方向?yàn)檎琘 方向?yàn)樨?fù),與理論分析麥克斯韋力分布相同。 所以,本文中所建立求解硅鋼片磁致伸縮力和麥克斯韋力的數(shù)值模型是正確的。
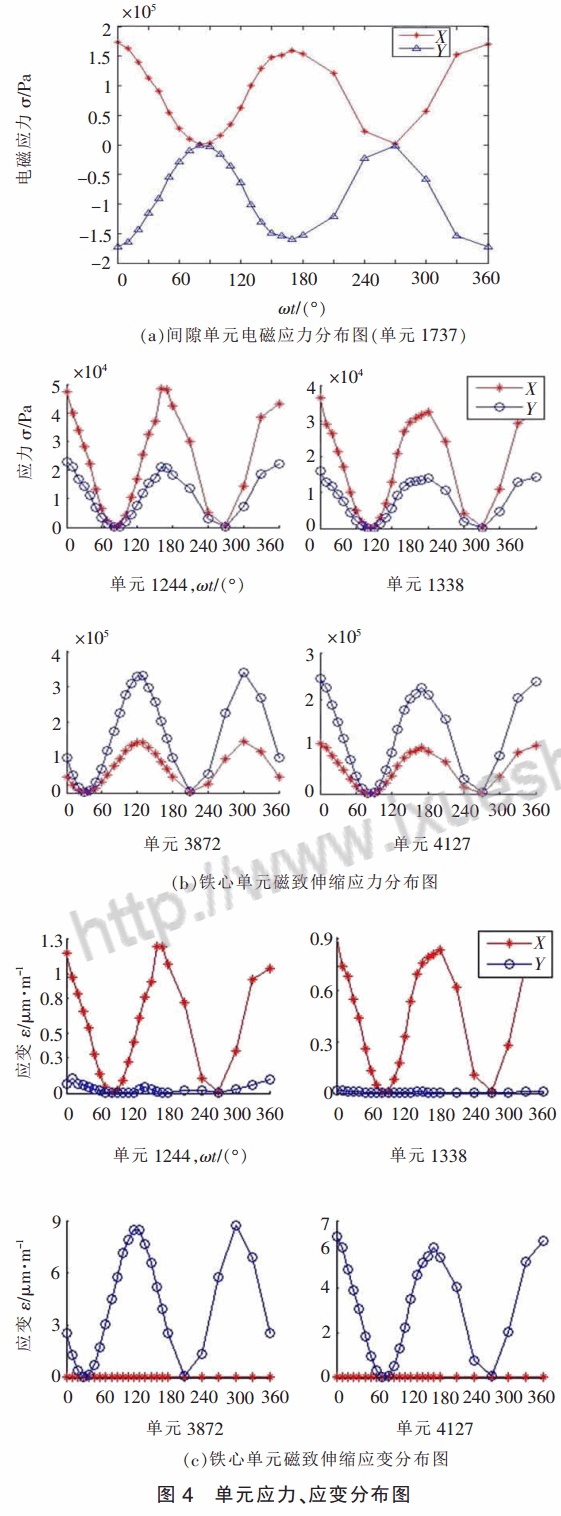
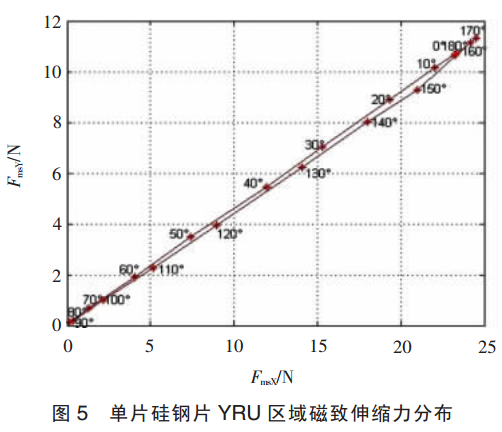
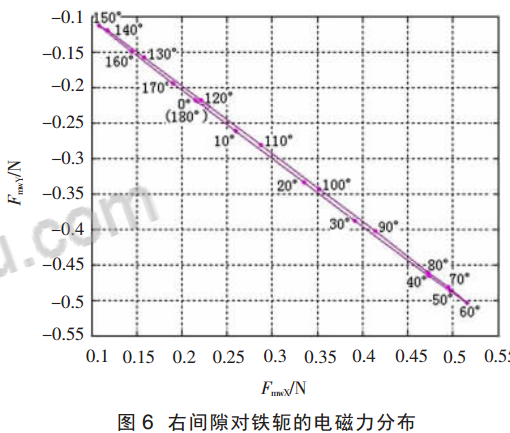
磁致伸縮力的計(jì)算結(jié)果圖 5 的分布規(guī)律與文獻(xiàn)[6]計(jì)算結(jié)果相同,數(shù)值大小由于計(jì)算所選鐵芯尺寸、區(qū)域大小以及硅鋼片數(shù)目、厚度不同而不同。 圖6 所示電磁力的計(jì)算結(jié)果表明間隙對(duì)鐵軛具有向下、向右的作用力,根據(jù)文獻(xiàn)[14]分析,其結(jié)果也是正確的。 顯然,磁致伸縮力大于電磁力,兩者的作用方向在不同相位時(shí)并不完全相同,換而言之,鐵芯的振動(dòng)并非各自振動(dòng)之和, 有時(shí)兩者會(huì)有相互減弱的效果。
文中筆者根據(jù)電磁場(chǎng)理論和彈性力學(xué)理論,建立了電磁—機(jī)械耦合數(shù)值模型, 求解電磁場(chǎng)時(shí)考慮了鐵芯硅鋼片應(yīng)力作用對(duì)導(dǎo)磁特性的影響; 推導(dǎo)了計(jì)算鐵芯取向硅鋼片磁致伸縮力的方程式。 將模型應(yīng)用于三相電力變壓器,將計(jì)算結(jié)果與測(cè)量、相關(guān)文獻(xiàn)和論著進(jìn)行了比較, 結(jié)果表明所建立的模型和求解方法是正確的, 為求解變壓器鐵芯磁致伸縮效應(yīng)提供了一種具有推廣應(yīng)用的數(shù)值計(jì)算方法。 計(jì)算結(jié)果同時(shí)也表明,對(duì)于變壓器結(jié)構(gòu),硅鋼片的磁致伸縮力遠(yuǎn)大于電磁力, 即用數(shù)值方法證明了變壓器本體噪聲主要是由鐵芯硅鋼片磁致伸縮引起的。
文獻(xiàn):
[1] Moses A J,Anderson P I, Phophongviwat T, et al. Contribution of magnetostriction to transformer noise[C]. UPEC2010 31st, 2010.
[2] Hori Y, Abe S, Sasaki M, et al. Vibration characteristics of transformer [C]. The papers of technical meetingon magnetics. IEE Japan, 1999.
[3] Phway T P P, Moses A J. Magnetisation induced mechanicalresonance in electrical steels [J]. J. Magn. &Magn. Mater., 2007,316(2):468-471.
[4] Moses A J. Measurement of magnetostriction and vibrationwith regard to transformer noise [J]. IEEE Trans.Magn.,1974, (10):154-156.
[5] Kitagawa W, Ishihara Y, Todaka T. Analysis of structural deformation and vibration of a transformer core by using magnetic property of magnetostriction [J]. Elect.Eng. in Japan, 2010,172(1):19-26.
[6] Kubiak W, Witczak P. Vibration analysis of small power transformer [J]. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2010,29(4):1116-1124.
[7] Moses A J, Phillips P S. Some effects of stress in Goss -oriented silicon -iron [J]. IEEE Trans. Magn.,1978,14(5):353-355.
[8] Anderson P I, Moses A J, Stanbury H J. Assessment of the stress sensitivity of magnetostriction in grain-oriented silicon steel[J]. IEEE Trans. Magn. 2007,43(8):3467-3476.
[9] Anderson P. Measurement of the stress sensitivity of magnetostriction in electrical steels under distorted waveform conditions [J]. J. Magn. & Magn. Mater.,2008,320:583-588.
[10] Stanbury H. Magnetostrictive effects at angles to the rolling direction in grain oriented silicon steel [D].Wales:University of Wales, 1984.
[11] Pitman K C. The influence of stress on ferromagnetic materials[J]. IEEE Trans. Magn. 1990,26(5):1978-1980.
[12] 楊伯源,張義同. 工程彈塑性力學(xué)[M]. 北京:機(jī)械工業(yè)出版社, 2003.
[13] Mohammed O A. Numerical prediction of magnetostrictive behavior in non-oriented electrical steel sheets[C].Southeast Con 2001.
[14] Mohammed O A, Liu S, Abed N. Study of the inverse magnetostriction effect on machine feformation [C].Southeast Con 2004.
[15] 顏威利,楊慶新,汪 友 華. 電氣工程電磁場(chǎng)數(shù)值分析[M].北京:機(jī)械工業(yè)出版社,2005.
[16] 辜承林,周可定,李郎如. 電力變壓器鐵芯磁場(chǎng)和損耗分布的三維數(shù)值方法與實(shí)施[J].中國(guó)電機(jī)工程學(xué)報(bào),1992,12(5):1-9.





